Основной причиной того, что верёвочные узлы не развязываются - это сила трения. Кто не знается сила трения - это сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению.
На Рис. 1 показана схема казачьего узла. Стрелками показаны силы, действующие на различные части узла, причём длина стрелок пропорциональна величине действующих сил. За счёт сил трения натяжение верёвки постепенно ослабевает, становясь равным нулю на свободной части ходового конца.
Т.к. сила трения между двумя поверхностями Fтр= μ・N, где μ - коэффициент трения, N-сила сдавливания поверхностей друг с другом. Таким образом, узел должен сжимать два конца верёвки, находящихся в противодвижении.
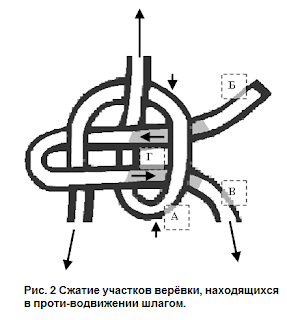
На Рис. 2 показано, как находящиеся в противодвижении части концы Б и В стягиваются петлёй А, создавая в области Г повышенное трение. Возникшее трение является трением покоя – конец Б остаётся неподвижным при затягивании узла.
На Рис. 3 показаны узлы для связывания двух верёвок. Пунктиром выделяются зоны трения. На Рис. 3-В видно, что концы в выделенных зонах прижимаются друг к другу при растягивании коренных концов. В узле Рис. 3-А верёвки находятся в противодвижении – узел держит, хотя и проскальзывает. В узле Рис. 3-Б в выделенной зоне оказываются концы, движущиеся в одном и том же направлении – верёвки легко скользят и узел не держит.
Современные верёвки изготавливаются из синтетических материалов. По сравнению со старыми верёвками из растительных волокон, они имеют меньший коэффициент трения и более растяжимы. Поэтому многие узлы, державшие на старых верёвках, на современных верёвках скользят или распускаются.
Другим способом увеличения силы трения является обнос верёвки вокруг какого-либо предмета. Сила трения в этом случае зависит от угла охвата предмета φ: Fтр=F1(1-e-μφ), где e=2.7, φ - в радианах.
На Рис. 1 показана схема казачьего узла. Стрелками показаны силы, действующие на различные части узла, причём длина стрелок пропорциональна величине действующих сил. За счёт сил трения натяжение верёвки постепенно ослабевает, становясь равным нулю на свободной части ходового конца.
 |
| 1 - коренной конец, 2 - ходовой конец, 4 - закрытая петля, 6 - обнос, 9 - предмет, вокруг которого завязывается узел |
Т.к. сила трения между двумя поверхностями Fтр= μ・N, где μ - коэффициент трения, N-сила сдавливания поверхностей друг с другом. Таким образом, узел должен сжимать два конца верёвки, находящихся в противодвижении.
На Рис. 2 показано, как находящиеся в противодвижении части концы Б и В стягиваются петлёй А, создавая в области Г повышенное трение. Возникшее трение является трением покоя – конец Б остаётся неподвижным при затягивании узла.
На Рис. 3 показаны узлы для связывания двух верёвок. Пунктиром выделяются зоны трения. На Рис. 3-В видно, что концы в выделенных зонах прижимаются друг к другу при растягивании коренных концов. В узле Рис. 3-А верёвки находятся в противодвижении – узел держит, хотя и проскальзывает. В узле Рис. 3-Б в выделенной зоне оказываются концы, движущиеся в одном и том же направлении – верёвки легко скользят и узел не держит.
Современные верёвки изготавливаются из синтетических материалов. По сравнению со старыми верёвками из растительных волокон, они имеют меньший коэффициент трения и более растяжимы. Поэтому многие узлы, державшие на старых верёвках, на современных верёвках скользят или распускаются.
Другим способом увеличения силы трения является обнос верёвки вокруг какого-либо предмета. Сила трения в этом случае зависит от угла охвата предмета φ: Fтр=F1(1-e-μφ), где e=2.7, φ - в радианах.
В таблице ниже показано ослабление натяжения верёвки в зависимости от числа оборотов вокруг предмета и коэффициента трения.
В ряде узлов трение усиливается дополнительным сдавливанием витков верёвки. При использовании этого метода натяжение ходового конца значительно ослабляется и его фиксация становится более эффективной (Рис. 5).
В ряде узлов трение усиливается дополнительным сдавливанием витков верёвки. При использовании этого метода натяжение ходового конца значительно ослабляется и его фиксация становится более эффективной (Рис. 5).




Комментариев нет:
Отправить комментарий