Измерения расстояний на карте

Отредактировано 22.09.2024

При измерении расстояний по топографической карте получают длины горизонтальных проекций, а не длины линий на земной поверхности.

Для измерения расстояний по карте используют миллиметровую или масштабную линейку, циркуль-измеритель, а для измерения кривых линий - курвиметр.

Измерение расстояний на карте миллиметровой линейкой

Миллиметровой линейкой (то есть той линейкой, на которой есть обозначения миллиметров) измерить расстояние между заданными точками на карте с точностью 0,1 см. Полученное число сантиметров умножить на величину именованного масштаба. Для равнинной местности результат будет соответствовать расстоянию на местности в метрах или километрах.

Пример.

На карте масштаба 1 : 50 000 (в 1 см - 500 м) расстояние между двумя точками равно 3,4 см. Определить расстояние между этими точками.
Решение. Именованный масштаб: в 1 см 500 м. Расстояние на местности между точками будет 3,4 × 500 = 1700 м.
При углах наклона земной поверхности более 10º необходимо ввести соответствующую поправку.

Измерение расстояний на карте циркулем-измерителем

При измерении расстояния по прямой линии иглы циркуля устанавливают на конечные точки, затем, не изменяя раствора циркуля, по линейному или поперечному масштабу отсчитывают расстояние. В том случае, когда раствор циркуля превышает длину линейного или поперечного масштаба, целое число километров определяется по квадратам координатной сетки, а остаток - обычным порядком по масштабу.

Измерение расстояний циркулем-измерителем по линейному масштабу

Для получения длины ломаной линии последовательно измеряют длину каждого её звена, а затем суммируют их величины. Такие линии измеряют также наращиванием раствора циркуля.

Длинные кривые отрезки измеряют по хордам шагами циркуля. Шаг циркуля (он выбирается в зависимости от извилистости линии), равный целому числу сотен или десятков метров, устанавливают с помощью поперечного или линейного масштаба. При перестановке ножек циркуля вдоль измеряемой линии в направлениях, показанных на рисунке ниже, б стрелками, считают шаги. Общая длина линии А1С1 складывается из отрезка А1В1, равного величине шага, умноженной на число шагов, и остатка В1С1 измеряемого по поперечному или линейному масштабу.

Измерение длины линии:
а - ломаной ABCD; б - кривойA1B1C1;  B'C' - вспомогательные точки

Пример.

Чтобы измерить длину ломаной АВСD (см. рис. выше, а), ножки циркуля сначала ставят в точки А и В. Затем, вращая циркуль вокруг точки В перемещают заднюю ножку из точки А в точку В', лежащую на продолжении прямой ВС.

Переднюю ножку из точки В переносят в точку С. В результате получают раствор циркуля В'С=АВ+ВС. Переместив аналогичным образом заднюю ножку циркуля из точки В' в точку С', а переднюю из С в D. получают раствор циркуля

С'D = В'С + СD, длину которого определяют с помощью поперечного или линейного масштаба.

Измерение расстояний на карте курвиметром

Кривые отрезки измеряют механическим или электронным курвиметром.

В механическом курвиметре колесико устанавливается на ноль вращая колесико рукой, а в электронном - нажав на кнопку сброса. Потом курвиметр ведётся колёсиком по кривой линии. Отсчет на циферблате против конца стрелки (в сантиметрах) умножают на величину масштаба карты и получают расстояние на местности. 

Для повышения точности и надежности результатов рекомендуется все измерения проводить дважды - в прямом и обратном направлениях. В случае незначительных различий измеренных данных за конечный результат принимается среднее арифметическое значение измеренных величин.

Точность измерения расстояний указанными способами с применением линейного масштаба составляет 0,5-1,0 мм в масштабе карты. То же самое, но с применением поперечного масштаба составляет 0,2-0,3 мм на 10 см длины линии.

Пересчет горизонтального проложения в наклонную дальность

Следует помнить, что в результате измерения расстояний по картам, получают длины горизонтальных проекций линий (d), а не длины линий на земной поверхности (S).

Наклонная дальность (S) и горизонтальное проложение (d)

Действительное расстояние на наклонной поверхности можно вычислить по формуле:

где:

      d - длина горизонтальной проекции линии S;

      α  - угол наклона земной поверхности.

Длину линии на топографической поверхности можно определить с помощью таблицы относительных величин поправок к длине горизонтального проложения (в %).

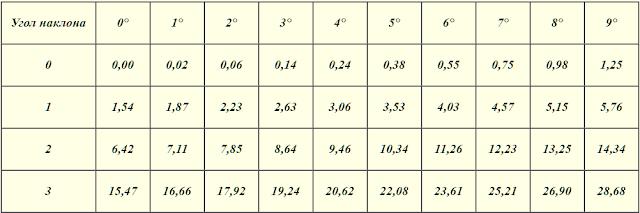
Правила пользования таблицей

1. В первой строке таблицы (0 десятков) приведены относительные величины поправок при углах наклона от 0° до 9°, во второй - от 10° до 19°, в третьей - от 20° до 29°, в четвертой - от 30° до 39°.

2. Чтобы определить абсолютную величину поправки, необходимо:

а) в таблице по углу наклона найти относительную величину поправки (если угол наклона топографической поверхности задан не целым числом градусов, то надо относительную величину поправки найти интерполированием между табличными величинами);

б) вычислить абсолютную величину поправки к длине горизонтального проложения (т. е. эту длину умножить на относительную величину поправки и полученное произведение разделить на 100).

3. Чтобы определить длину линии на топографической поверхности, надо вычисленную абсолютную величину поправки прибавить к длине горизонтального проложения.

Пример. На топографической карте определена длина горизонтального проложения 1735 м, угол наклона топографической поверхности - 7°15′. В таблице относительные величины поправок приведены для целых градусов. Следовательно, для 7°15' необходимо определить ближайшую большую и ближайшую меньшую величины кратные одному градусу - 8º и 7º:

• для 8° относительная величина поправки - 0,98%;
• для 7° - 0,75%;
• разность табличных величин в 1º (60′) - 0,23%;
• разность между заданным углом наклона земной поверхности 7°15' и ближайшей меньшей табличной величиной 7º составляет 15'.

Составляем пропорции и находим относительную величину поправки для 15':

Для 60′ поправка составляет - 0,23%;

Для 15′ поправка составляет - х%

Относительная величина поправки для угла наклона 7°15'

                             0,75%+0,06% = 0,81%

Затем надо определить абсолютную величину поправки:

                         

Длина наклонной линии на топографической поверхности будет:

                         1735 м + 14 м = 1749 м.

При малых углах наклона (менее 4° - 5°) разница в длине наклонной линии и ее горизонтальной проекции очень мала и может не учитываться.

Точность измерения расстояний по карте

Опытным путем установлено, что с помощью циркуля измерения прямолинейных отрезков на карте не могут быть выполнены точнее, чем 0,2 мм. Расстояние на местности, соответствующее 0,2 мм на карте, называют предельной точностью масштаба карты.

Однако точность определения расстояний по карте зависит не только от точности измерений, но и от погрешностей самой карты, неизбежных при ее составлении и печатании, которые могут достигать 0,5 мм, а на картах горных районов - 0,75 мм. Источниками ошибок измерений являются также помятость и деформация бумаги.

С учётом этого фактическая точность измерения прямых линий по карте, как показывает практика, колеблется в пределах 0,5-1,0 мм, что в масштабе 1:25000 на местности составляет 12-25 м, в масштабе 1:50000 - 25-50 м, 1:100000 - 50-100 м.